Pada teorema ini hanya berlaku
untuk rangkaian yang bersifat linier, dimana rangkaian linier adalah suatu
rangkaian dimana persamaan yang muncul akan memenuhi jika y = kx, dimana k =
konstanta dan x = variabel. Dalam setiap rangkaian linier dengan beberapa buah
sumber tegangan/ sumber arus dapat dihitung dengan cara:
Menjumlah aljabarkan tegangan/ arus yang disebabkan
tiap sumber independent / bebas yang bekerja sendiri, dengan semua sumber
tegangan / arus independent / bebas lainnya diganti dengan tahanan dalamnya.
Pengertian dari teorema diatas
bahwa jika terdapat n buah sumber bebas maka dengan teorema superposisi
samadengan n buah keadaan rangkaian yang dianalisis, dimana nantinya n buah
keadaan tersebut akan dijumlahkan. Jika terdapat beberapa buah sumber tak bebas
maka tetap saja teorema superposisi menghitung untuk n buah keadaan dari n buah
sumber yang bebasnya.
Rangkaian linier
tentu tidak terlepas dari gabungan rangkaian yang mempunyai sumber independent
atau sumber bebas, sumber dependent / sumber tak bebas linier
(sumber dependent arus / tegangan sebanding dengan pangkat satu dari
tegangan/ arus lain, atau sebanding dengan jumlah pangkat satu besaran-besaran
tersebut) dan elemen resistor (R ), induktor ( L ), dan kapasitor ( C ).
Contoh latihan :
1. Berapakah
arus "i" dengan teorema superposisi
Jawaban :
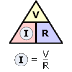
(i) Pada saat sumber tegangan aktif/bekerja maka
sumber arus tidak aktif (diganti dengan tahanan dalamnya yaitu tak hingga atau
rangkaian open circuit). (ii) Pada saat sumber arus aktif atau bekerja maka sumber tegangan tidak aktif(diganti dngan tahanan dalamnya yaitu nol atau rangkaian short circuit).


0 Comments